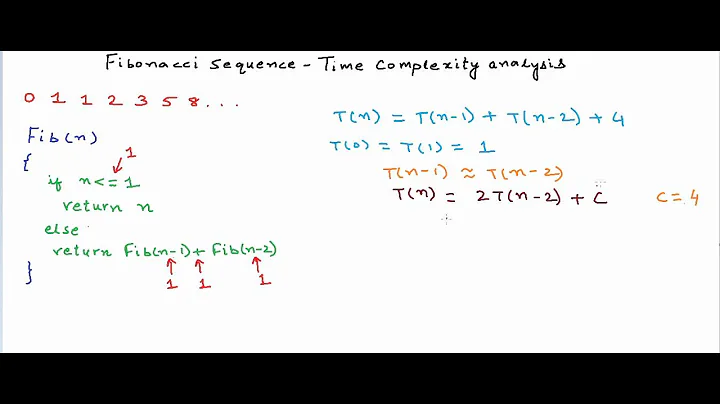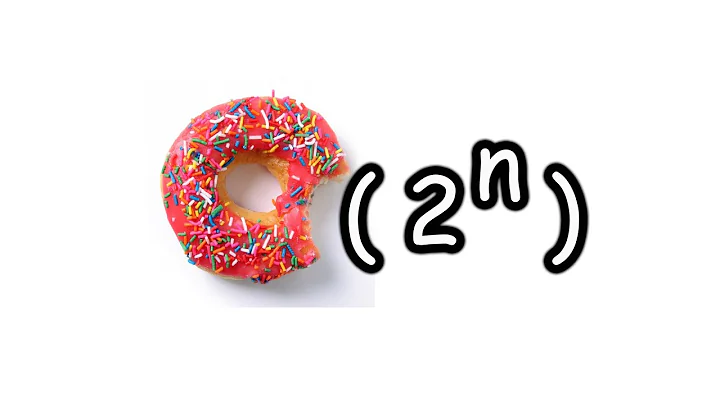Big-O for various Fibonacci Implementations
The recursive version is not polynomial time - it's exponential, tightly bounded at φn where φ is the golden ratio (≈ 1.618034). The recursive version will use O(n) memory (the usage comes from the stack).
The memoization version will take O(n) time on first run, since each number is only computed once. However, in exchange, it also take O(n) memory for your current implementation (the n comes from storing the computed value, and also for the stack on the first run). If you run it many times, the time complexity will become O(M + q) where M is the max of all input n and q is the number of queries. The memory complexity will become O(M), which comes from the array which holds all the computed values.
The iterative implementation is the best if you consider one run, as it also runs in O(n), but uses constant amount of memory O(1) to compute. For a large number of runs, it will recompute everything, so its performance may not be as good as memoization version.
(However, practically speaking, long before the problem of performance and memory, the number is likely to overflow even 64-bit integer, so an accurate analysis must take into account the time it takes to do addition if you are computing the full number).
As plesiv mentioned, the Fibonacci number can also be computed in O(log n) by matrix multiplication (using the same trick as fast exponentiation by halving the exponent at every step).
Related videos on Youtube
Nayuki
I write programs and do math for fun. See my website for articles: https://www.nayuki.io/
Updated on September 14, 2022Comments
-
Nayuki over 1 year
I just tried implementing code (in Java) for various means by which the nth term of the Fibonacci sequence can be computed and I'm hoping to verify what I've learnt.
The iterative implementation is as follows:
public int iterativeFibonacci(int n) { if ( n == 1 ) return 0; else if ( n == 2 ) return 1; int i = 0, j = 1, sum = 0; for ( ; (n-2) != 0; --n ) { sum = i + j; i = j; j = sum; } return sum; }The recursive implementation is as follows :-
public int recursiveFibonacci(int n) { if ( n == 1 ) return 0; else if ( n == 2 ) return 1; return recursiveFibonacci(n-1) + recursiveFibonacci(n-2); }The memoized implementation is as follows :-
public int memoizedFibonacci(int n) { if ( n <= 0 ) return -1; else if ( n == 1 ) return 0; else if ( n == 2 ) return 1; if ( memory[n-1] == 0 ) memory[n-1] = memoizedFibonacci(n-1); if ( memory[n-2] == 0 ) memory[n-2] = memoizedFibonacci(n-2); return memory[n-1]+memory[n-2]; }I'm having a bit of a doubt when trying to figure out the Big-O of these implementations. I believe the iterative implementation to be O(n) as it loops through N-2 times.
In the recursive function, there are values recomputed, hence I think it's O(n^2).
In the memoized function, more than half of the values are accessed based on memoization. I've read that an algorithm is O(log N) if it takes constant time to reduce the problem space by a fraction and that an algorithm is O(N) if it takes constant time to reduce the problem space by a constant amount. Am I right in believing that the memoized implementation is O(n) in complexity? If so, wouldn't the iterative implementation be the best among all three? (as it does not use the additional memory that memoization requires).
-
 plesiv over 11 yearsLinear recurence problems like these in programming competitions are usually solved via "matrix exponentiation". There's a C++ example for Fibonacci series in this blogpost.
plesiv over 11 yearsLinear recurence problems like these in programming competitions are usually solved via "matrix exponentiation". There's a C++ example for Fibonacci series in this blogpost.
-