Big O Notation - O(nlog(n)) vs O(log(n^2))

Question

Is the notation of NLog(N) the same as Log(N^2)? If so, why is it not written like that?

Is NLog(N) the standard notation? I feel like Log(N^2) is less confusing to see.

Solution 1

• O(log(n^2)) is simply O(2 log(n)) = O(log(n)). It is a logarithmic function. Its value is much smaller than the linear function O(n).

• O(n log(n)) is a larger function. Its values are larger than the linear function O(n)

They are completely different functions (and different big-O complexities). O(n log(n)) is much larger than O(log(n^2))

This plot shows the difference:

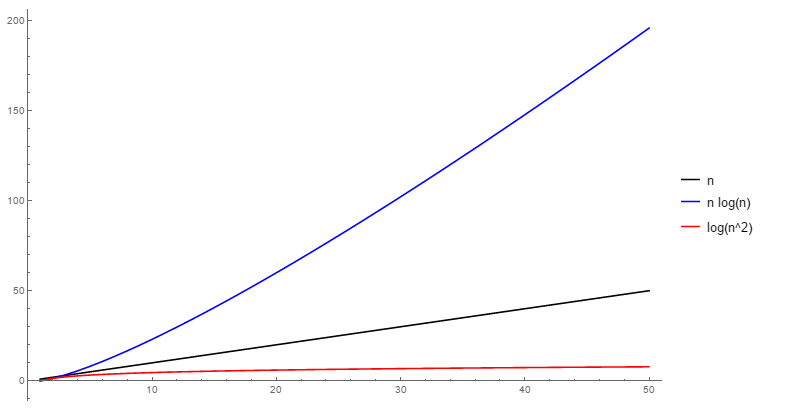
Solution 2

Adding logarithms is the same as multiplying numbers, so log(n*n) becomes log(n) + log(n) = 2 log(n).

n log(n) is close to linear. The first n is the important part, as the rest of it grows rather slowly.

For example merge sort has n log n time complexity, because if you think of the merging as a tree, then the tree is log(n) levels tall, and on each level all n elements are processed.