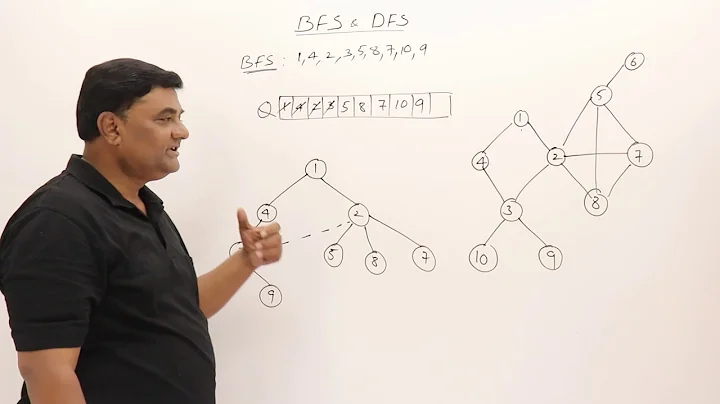
Breadth First Search time complexity analysis

Question

The time complexity to go over each adjacent edge of a vertex is, say, O(N), where N is number of adjacent edges. So, for V numbers of vertices the time complexity becomes O(V*N) = O(E), where E is the total number of edges in the graph. Since removing and adding a vertex from/to a queue is O(1), why is it added to the overall time complexity of BFS as O(V+E)?

Solution 1

I hope this is helpful to anybody having trouble understanding computational time complexity for Breadth First Search a.k.a BFS.

Queue graphTraversal.add(firstVertex);

// This while loop will run V times, where V is total number of vertices in graph.
while(graphTraversal.isEmpty == false)

    currentVertex = graphTraversal.getVertex();

    // This while loop will run Eaj times, where Eaj is number of adjacent edges to current vertex.
    while(currentVertex.hasAdjacentVertices)
        graphTraversal.add(adjacentVertex);

    graphTraversal.remove(currentVertex);

Time complexity is as follows:

V * (O(1) + O(Eaj) + O(1))
V + V * Eaj + V
2V + E(total number of edges in graph)
V + E

I have tried to simplify the code and complexity computation but still if you have any questions let me know.

Solution 2

Considering the following Graph we see how the time complexity is O(|V|+|E|) but not O(V*E).

Adjacency List

V     E
v0:{v1,v2} 
v1:{v3}
v2:{v3}
v3:{}

Operating How BFS Works Step by Step

Step1:

Adjacency lists:

V     E
v0: {v1,v2} mark, enqueue v0
v1: {v3}
v2: {v3}
v3: {}

Step2:

Adjacency lists:

V     E
v0: {v1,v2} dequeue v0;mark, enqueue v1,v2
v1: {v3}
v2: {v3}
v3: {}

Step3:

Adjacency lists:

V     E
v0: {v1,v2}
v1: {v3} dequeue v1; mark,enqueue v3
v2: {v3}
v3: {}

Step4:

Adjacency lists:

V     E
v0: {v1,v2}
v1: {v3}
v2: {v3} dequeue v2, check its adjacency list (v3 already marked)
v3: {}

Step5:

Adjacency lists:

V     E
v0: {v1,v2}
v1: {v3}
v2: {v3}
v3: {} dequeue v3; check its adjacency list

Step6:

Adjacency lists:

V     E
v0: {v1,v2} |E0|=2
v1: {v3}    |E1|=1
v2: {v3}    |E2|=1
v3: {}      |E3|=0

Total number of steps:

|V| + |E0| + |E1| + |E2| +|E3| == |V|+|E|
 4  +  2   +  1   +   1  + 0   ==  4 + 4
                           8   ==  8

Assume an adjacency list representation, V is the number of vertices, E the number of edges.

Each vertex is enqueued and dequeued at most once.

Scanning for all adjacent vertices takes O(|E|) time, since sum of lengths of adjacency lists is |E|.

Hence The Time Complexity of BFS Gives a O(|V|+|E|) time complexity.

Solution 3

The other answers here do a great job showing how BFS runs and how to analyze it. I wanted to revisit your original mathematical analysis to show where, specifically, your reasoning gives you a lower estimate than the true value.

Your analysis goes like this:

• Let N be the average number of edges incident to each node (N = E / V).
• Each node, therefore, spends O(N) time doing operations on the queue.
• Since there are V nodes, the total runtime is the O(V) · O(N) = O(V) · O(E / V) = O(E).

You are very close to having the right estimate here. The question is where the missing V term comes from. The issue here is that, weirdly enough, you can't say that O(V) · O(E / V) = O(E).

You are totally correct that the average work per node is O(E / V). That means that the total work done asympotically is bounded from above by some multiple of E / V. If we think about what BFS is actually doing, the work done per node probably looks more like c₁ + c₂E / V, since there's some baseline amount of work done per node (setting up loops, checking basic conditions, etc.), which is what's accounted for by the c₁ term, plus some amount of work proportional to the number of edges visited (E / V, times the work done per edge). If we multiply this by V, we get that

V · (c₁ + c₂E / V)

= c₁V + c₂E

= Θ(V + E)

What's happening here is that those lovely lower-order terms that big-O so conveniently lets us ignore are actually important here, so we can't easily discard them. So that's mathematically at least what's going on.

What's actually happening here is that no matter how many edges there are in the graph, there's some baseline amount of work you have to do for each node independently of those edges. That's the setup to do things like run the core if statements, set up local variables, etc.

Solution 4

Performing an O(1) operation L times, results to O(L) complexity. Thus, removing and adding a vertex from/to the Queue is O(1), but when you do that for V vertices, you get O(V) complexity. Therefore, O(V) + O(E) = O(V+E)

Solution 5

Will the time complexity of BFS be not O(V) considering we only have to traverse the vertices in the adjacency list? Am I missing something here?

For the below graph represented using adjacency list for ex:

   0 ->1->2->null
   1->3->4->null
   3->null
   4->null

While creating the graph we have the adjacency list which is an array of linked lists. So my understanding is during traversal this array is available to us and it's enough if we only traverse all the elements of this array and mark each element as visited to not visit it twice. What am I missing here? 

View more solutions

Comments

[Pranav Nandan]

Thanks, Nice explanation.

[ajfigueroa]

This was really helpful some 2 years later, thanks! Should the Eaj portion in the equation be wrapped as O(Eaj) though?

[Palak Jain]

Yes @ajfigueroa

[Neeraj Sonaniya]

One thing we can add that 'Eaj' max could be 'V-1' (total vertices in case of fully connected graph) and Min 0 (In case of disconnected graph), in that case equation: V * Eaj + 2V for max = 2V + V(V-1) = O(V^2) and for min O(V).

[benji]

O(1) + O(Eaj) + O(1) is not just O(Eaj)?

[Daniel Nitzan]

It should be noted that in order avoid cycles or visiting vertices multiple times, visited vertices should be marked

[Tyler2P]

Hi and welcome to Stack Overflow! Please take the tour. Thanks for answering but can you also add an explanation on how your code solves the issue? Check the help center for info on how to format your answer.

[mathguy]

The answer is mostly correct, but your notation is not. Specifically the V * Eaj part. The calculation is a sum over all vertices, not a multiplication by V. Summing O(1) over V is O(V) (even that is not entirely correct - the "O(1)" must be uniformly bounded over all vertices, which is not obvious); but the sum of Eaj is E - and that is the correct computation - while if you were to sum V * Eaj you would get V * E. It's just bad notation though, not something incorrect in the thought process.