Finding longest common subsequence in O(NlogN) time

Question

Is there any way of finding the longest common subsequence of two sequences in O(NlogN) time?

I read somewhere that there is a way to achieve this using binary search.

I know the dp approach that takes O(N²) time.

Solution 1

For the general case, the O(N^2) dynamic programming algorithm is the best you can do. However, there exist better algorithms in some special cases.

1. Alphabet size is bounded

This is a very common situation. Sequences consisting of letters from some alphabet (e.g. English) lie in this category. For this case, the O(N*M) algorithm can be optimised to get an O(N^2/logN) with method of four Russians. I don't know how exactly, you can search for it.

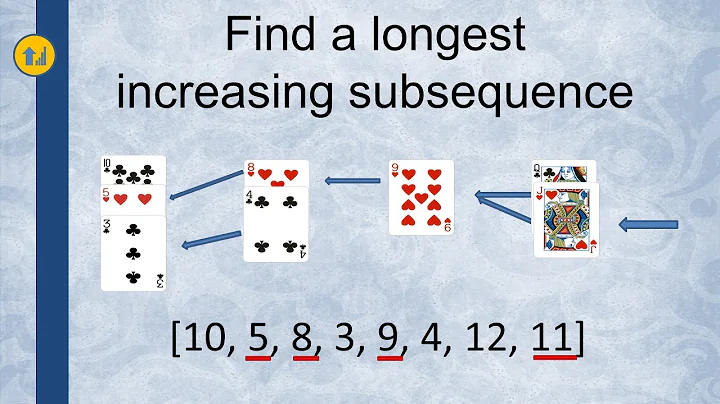
2. Both sequences consist of distinct elements

An example problem is "Given two permutations of numbers from 1 to N, find their LCS". This one can be solved in O(N*logN).
Let the sequences be A and B.
Define a sequence C. C[i] is the index of B[i] in A. (A[C[i]] = B[i])
LCS of A and B is the longest increasing subsequence of C.

Solution 2

The dynamic programming approach, which is O(n²) for general case. For certain other cases, there are lower-complexity algorithms:

• For a fixed alphabet size (which doesn't grow with n), there's the Method of Four Russians which brings the time down to O(n²/log n) (see here).

• See here another further optimized case.

Solution 3

Assuming Exponential Time Hypothesis (which is stricter than P is not equal to NP, but is still widely believed to be true), it is not possible to do it in time O(N^{2 - eps}) for any positive constant eps, see "Quadratic Conditional Lower Bounds for String Problems and Dynamic Time Warping" by Karl Bringmann and Marvin Kunnemann (pre-print on arXiv is available).

Roughly speaking, it means that the general case of this problem cannot be solved in time better than something like O(N^2/log N), so if you want faster algorithms you have to consider additional constraints (some properties of the strings) or look for approximate solution.

Solution 4

The longest common subsequence between two sequences is essentially n-squared.

Masek and Patterson (1980) made a minor improvement to n-squared / log n using the so-called "Four Russians" technique.

In most cases the additional complexity introduced by such convoluted approaches is not justified by the small gains. For practical purposes you can consider the n-squared approach as the reasonable optimum in typical applications.

View more solutions

Comments

[Ankit Roy]

There's also the very practical O(nd) approach of Meyers, where d is the Levenshtein distance between the two strings -- this is O(n) if there are a bounded number of differences. TTBOMK it's still what's used in diff.

[dpm]

The second case requires only one string to have distinct elements.