How can I calculate the area of a bezier curve?

javascript svg

10,840

Solution 1

Convert the path to a polygon of arbitrary precision, and then calculate the area of the polygon.

~~Interactive Demo: Area of Path via Subdivision~~ _(broken)

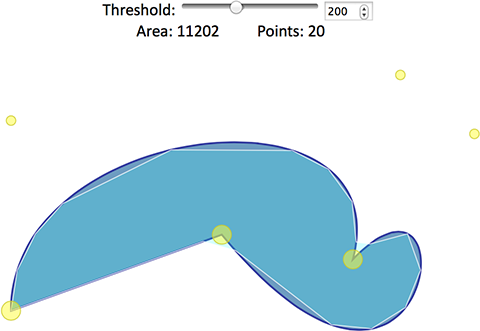
Screenshot of Demo

At its core the above demo uses functions for adaptively subdividing path into a polygon and computing the area of a polygon:

// path:      an SVG <path> element
// threshold: a 'close-enough' limit (ignore subdivisions with area less than this)
// segments:  (optional) how many segments to subdivisions to create at each level
// returns:   a new SVG <polygon> element
function pathToPolygonViaSubdivision(path,threshold,segments){
  if (!threshold) threshold = 0.0001; // Get really, really close
  if (!segments)  segments = 3;       // 2 segments creates 0-area triangles
  var points = subdivide( ptWithLength(0), ptWithLength( path.getTotalLength() ) );
  for (var i=points.length;i--;) points[i] = [points[i].x,points[i].y];
  var doc  = path.ownerDocument;
  var poly = doc.createElementNS('http://www.w3.org/2000/svg','polygon');
  poly.setAttribute('points',points.join(' '));
  return poly;
  // Record the distance along the path with the point for later reference
  function ptWithLength(d) {
    var pt = path.getPointAtLength(d); pt.d = d; return pt;
  }
  // Create segments evenly spaced between two points on the path.
  // If the area of the result is less than the threshold return the endpoints.
  // Otherwise, keep the intermediary points and subdivide each consecutive pair.
  function subdivide(p1,p2){
    var pts=[p1];
    for (var i=1,step=(p2.d-p1.d)/segments;i<segments;i++){
      pts[i] = ptWithLength(p1.d + step*i);
    }
    pts.push(p2);
    if (polyArea(pts)<=threshold) return [p1,p2];
    else {
      var result = [];
      for (var i=1;i<pts.length;++i){
        var mids = subdivide(pts[i-1], pts[i]);
        mids.pop(); // We'll get the last point as the start of the next pair
        result = result.concat(mids)
      }
      result.push(p2);
      return result;
    }
  }
  // Calculate the area of an polygon represented by an array of points
  function polyArea(points){
    var p1,p2;
    for(var area=0,len=points.length,i=0;i<len;++i){
      p1 = points[i];
      p2 = points[(i-1+len)%len]; // Previous point, with wraparound
      area += (p2.x+p1.x) * (p2.y-p1.y);
    }
    return Math.abs(area/2);
  }
}

// Return the area for an SVG <polygon> or <polyline>
// Self-crossing polys reduce the effective 'area'
function polyArea(poly){
  var area=0,pts=poly.points,len=pts.numberOfItems;
  for(var i=0;i<len;++i){
    var p1 = pts.getItem(i), p2=pts.getItem((i+-1+len)%len);
    area += (p2.x+p1.x) * (p2.y-p1.y);
  }
  return Math.abs(area/2);
}

Following is the original answer, which uses a different (non-adaptive) technique for converting the <path> to a <polygon>.

~~Interactive Demo: http://phrogz.net/svg/area_of_path.xhtml~~ _(broken)

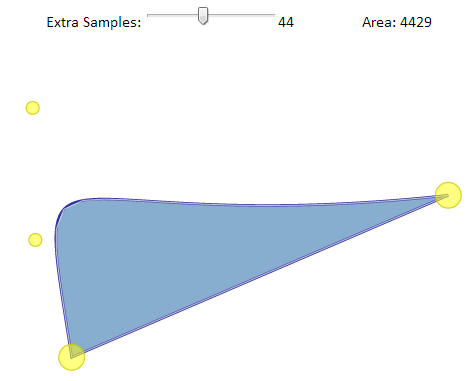
Screenshot of Demo

At its core the above demo uses functions for approximating a path with a polygon and computing the area of a polygon.

// Calculate the area of an SVG polygon/polyline
function polyArea(poly){
  var area=0,pts=poly.points,len=pts.numberOfItems;
  for(var i=0;i<len;++i){
    var p1 = pts.getItem(i), p2=pts.getItem((i+len-1)%len);
    area += (p2.x+p1.x) * (p2.y-p1.y);
  }
  return Math.abs(area/2);
}
// Create a <polygon> approximation for an SVG <path>
function pathToPolygon(path,samples){
  if (!samples) samples = 0;
  var doc = path.ownerDocument;
  var poly = doc.createElementNS('http://www.w3.org/2000/svg','polygon');
  // Put all path segments in a queue
  for (var segs=[],s=path.pathSegList,i=s.numberOfItems-1;i>=0;--i)
    segs[i] = s.getItem(i);
  var segments = segs.concat();
  var seg,lastSeg,points=[],x,y;
  var addSegmentPoint = function(s){
    if (s.pathSegType == SVGPathSeg.PATHSEG_CLOSEPATH){
    }else{
      if (s.pathSegType%2==1 && s.pathSegType>1){
        x+=s.x; y+=s.y;
      }else{
        x=s.x; y=s.y;
      }          
      var last = points[points.length-1];
      if (!last || x!=last[0] || y!=last[1]) points.push([x,y]);
    }
  };
  for (var d=0,len=path.getTotalLength(),step=len/samples;d<=len;d+=step){
    var seg = segments[path.getPathSegAtLength(d)];
    var pt  = path.getPointAtLength(d);
    if (seg != lastSeg){
      lastSeg = seg;
      while (segs.length && segs[0]!=seg) addSegmentPoint( segs.shift() );
    }
    var last = points[points.length-1];
    if (!last || pt.x!=last[0] || pt.y!=last[1]) points.push([pt.x,pt.y]);
  }
  for (var i=0,len=segs.length;i<len;++i) addSegmentPoint(segs[i]);
  for (var i=0,len=points.length;i<len;++i) points[i] = points[i].join(',');
  poly.setAttribute('points',points.join(' '));
  return poly;
}

Solution 2

I hesitated to just make a comment or a full reply. But a simple Google search of "area bezier curve" results in the first three links (the first one being this same post), in :

http://objectmix.com/graphics/133553-area-closed-bezier-curve.html (archived)

that provides the closed form solution, using the divergence theorem. I am surprised that this link has not been found by the OP.

Copying the text in case the website goes down, and crediting the author of the reply Kalle Rutanen:

An interesting problem. For any piecewise differentiable curve in 2D, the following general procedure gives you the area inside the curve / series of curves. For polynomial curves (Bezier curves), you will get closed form solutions.

Let g(t) be a piecewise differentiable curve, with 0 <= t <= 1. g(t) is oriented clockwise and g(1) = g(0).

Let F(x, y) = [x, y] / 2

Then div(F(x, y)) = 1 where div is for divergence.

Now the divergence theorem gives you the area inside the closed curve g (t) as a line integral along the curve:

int(dot(F(g(t)), perp(g'(t))) dt, t = 0..1) = (1 / 2) * int(dot(g(t), perp(g'(t))) dt, t = 0..1)

perp(x, y) = (-y, x)

where int is for integration, ' for differentiation and dot for dot product. The integration has to be pieced to the parts corresponding to the smooth curve segments.

Now for examples. Take the Bezier degree 3 and one such curve with control points (x0, y0), (x1, y1), (x2, y2), (x3, y3). The integral over this curve is:

I := 3 / 10 * y1 * x0 - 3 / 20 * y1 * x2 - 3 / 20 * y1 * x3 - 3 / 10 * y0 * x1 - 3 / 20 * y0 * x2 - 1 / 20 * y0 * x3 + 3 / 20 * y2 * x0 + 3 / 20 * y2 * x1 - 3 / 10 * y2 * x3 + 1 / 20 * y3 * x0 + 3 / 20 * y3 * x1 + 3 / 10 * y3 * x2

Calculate this for each curve in the sequence and add them up. The sum is the area enclosed by the curves (assuming the curves form a loop).

If the curve consists of just one Bezier curve, then it must be x3 = x0 and y3 = y0, and the area is:

Area := 3 / 20 * y1 * x0 - 3 / 20 * y1 * x2 - 3 / 20 * y0 * x1 + 3 / 20 * y0 * x2 - 3 / 20 * y2 * x0 + 3 / 20 * y2 * x1

Hope I did not do mistakes.

--
Kalle Rutanen
http://kaba.hilvi.org

Solution 3

I had the same problem but I am not using javascript so I cannot use the accepted answer of @Phrogz. ~~In addition the SVGPathElement.getPointAtLength() which is used in the accepted answer is deprecated according to Mozilla.~~

When describing a Bézier curve with the points (x0/y0), (x1/y1), (x2/y2) and (x3/y3) (where (x0/y0) is the start point and (x3/y3) the end point) you can use the parametrized form:

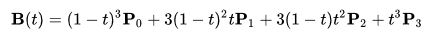^{(source: Wikipedia)}

with B(t) being the point on the Bézier curve and P_i the Bézier curve defining point (see above, P₀ is the starting point, ...). t is the running variable with 0 ≤ t ≤ 1.

This form makes it very easy to approximate a Bézier curve: You can generate as much points as you want by using t = i / n_points. (Note that you have to add the start and the end point). The result is a polygon. You can then use the shoelace formular (like @Phrogz did in his solution) to calculate the area. Note that for the shoelace formular the order of the points is important. By using t as the parameter the order will always be correct.

To match the question here is an interactive example in the code snippet, also written in javascript. This can be adopted to other languages. It does not use any javascript (or svg) specific commands (except for the drawings). Note that this requires a browser which supports HTML5 to work.

/**
 *  Approximate the bezier curve points.
 *
 *  @param bezier_points: object, the points that define the
 *                          bezier curve
 *  @param point_number:  int, the number of points to use to
 *                          approximate the bezier curve
 *
 *  @return Array, an array which contains arrays where the 
 *    index 0 contains the x and the index 1 contains the 
 *     y value as floats
 */
function getBezierApproxPoints(bezier_points, point_number){
  if(typeof bezier_points == "undefined" || bezier_points === null){
    return [];
  }
  var approx_points = [];
  // add the starting point
  approx_points.push([bezier_points["x0"], bezier_points["y0"]]);
  // implementation of the bezier curve as B(t), for futher
  // information visit 
  // https://wikipedia.org/wiki/B%C3%A9zier_curve#Cubic_B%C3%A9zier_curves
  var bezier = function(t, p0, p1, p2, p3){
    return Math.pow(1 - t, 3) * p0 + 
      3 * Math.pow(1 - t, 2) * t * p1 + 
      3 * (1 - t) * Math.pow(t, 2) * p2 + 
      Math.pow(t, 3) * p3;
  };
  // Go through the number of points, divide the total t (which is 
  // between 0 and 1) by the number of points. (Note that this is 
  // point_number - 1 and starting at i = 1 because of adding the
  // start and the end points.)
  // Also note that using the t parameter this will make sure that 
  // the order of the points is correct.
  for(var i = 1; i < point_number - 1; i++){
    let t = i / (point_number - 1);
    approx_points.push([
      // calculate the value for x for the current t
      bezier(
        t, 
        bezier_points["x0"], 
        bezier_points["x1"], 
        bezier_points["x2"], 
        bezier_points["x3"]
      ),
      // calculate the y value
      bezier(
        t, 
        bezier_points["y0"], 
        bezier_points["y1"], 
        bezier_points["y2"], 
        bezier_points["y3"]
      )
    ]);
  }
  // Add the end point. Note that it is important to do this 
  // **after** the other points. Otherwise the polygon will 
  // have a weird form and the shoelace formular for calculating
  // the area will get a weird result.
  approx_points.push([bezier_points["x3"], bezier_points["y3"]]);
  return approx_points;
}
/**
 *  Get the bezier curve values of the given path.
 *
 *  The returned array contains objects where each object 
 *  describes one cubic bezier curve. The x0/y0 is the start 
 *  point and the x4/y4 is the end point. x1/y1 and x2/y2 are 
 *  the control points.
 *
 *  Note that a path can also contain other objects than 
 *  bezier curves. Arcs, quadratic bezier curves and lines 
 *  are ignored.
 *
 *  @param svg:     SVGElement, the svg
 *  @param path_id: String, the id of the path element in the
 *                    svg
 *
 *  @return array, an array of plain objects where each 
 *    object represents one cubic bezier curve with the values 
 *    x0 to x4 and y0 to y4 representing the x and y 
 *    coordinates of the points
 */
function getBezierPathPoints(svg, path_id){
  var path = svg.getElementById(path_id);
  if(path === null || !(path instanceof SVGPathElement)){
    return [];
  }
  var path_segments = splitPath(path);
  var points = [];
  var x = 0;
  var y = 0;
  for(index in path_segments){
    if(path_segments[index]["type"] == "C"){
      let bezier = {};
      // start is the end point of the last element
      bezier["x0"] = x;
      bezier["y0"] = y;
      bezier["x1"] = path_segments[index]["x1"];
      bezier["y1"] = path_segments[index]["y1"];
      bezier["x2"] = path_segments[index]["x2"];
      bezier["y2"] = path_segments[index]["y2"];
      bezier["x3"] = path_segments[index]["x"];
      bezier["y3"] = path_segments[index]["y"];
      points.push(bezier);
    }
    x = path_segments[index]["x"];
    y = path_segments[index]["y"];
  }
  return points;
}
/**
 *  Split the given path to the segments.
 *
 *  @param path:           SVGPathElement, the path
 *
 *  @return object, the split path `d`
 */
function splitPath(path){
  let d = path.getAttribute("d");
  d = d.split(/\s*,|\s+/);
  let segments = [];
  let segment_names = {
    "M": ["x", "y"],
    "m": ["dx", "dy"],
    "H": ["x"],
    "h": ["dx"],
    "V": ["y"],
    "v": ["dy"],
    "L": ["x", "y"],
    "l": ["dx", "dy"],
    "Z": [],
    "C": ["x1", "y1", "x2", "y2", "x", "y"],
    "c": ["dx1", "dy1", "dx2", "dy2", "dx", "dy"],
    "S": ["x2", "y2", "x", "y"],
    "s": ["dx2", "dy2", "dx", "dy"],
    "Q": ["x1", "y1", "x", "y"],
    "q": ["dx1", "dy1", "dx", "dy"],
    "T": ["x", "y"],
    "t": ["dx", "dy"],
    "A": ["rx", "ry", "rotation", "large-arc", "sweep", "x", "y"],
    "a": ["rx", "ry", "rotation", "large-arc", "sweep", "dx", "dy"]
  };
  let current_segment_type;
  let current_segment_value;
  let current_segment_index;
  for(let i = 0; i < d.length; i++){
    if(typeof current_segment_value == "number" && current_segment_value < segment_names[current_segment_type].length){
      let segment_values = segment_names[current_segment_type];
      segments[current_segment_index][segment_values[current_segment_value]] = d[i];
      current_segment_value++;
    }
    else if(typeof segment_names[d[i]] !== "undefined"){
      current_segment_index = segments.length;
      current_segment_type = d[i];
      current_segment_value = 0;
      segments.push({"type": current_segment_type});
    }
    else{
      delete current_segment_type;
      delete current_segment_value;
      delete current_segment_index;
    }
  }
  return segments;
}
/**
 *  Calculate the area of a polygon. The pts are the 
 *  points which define the polygon. This is
 *  implementing the shoelace formular.
 *
 *  @param pts: Array, the points
 *
 *  @return float, the area
 */
function polyArea(pts){
  var area = 0;
  var n = pts.length;
  for(var i = 0; i < n; i++){
    area += (pts[i][1] + pts[(i + 1) % n][1]) * (pts[i][0] - pts[(i + 1) % n][0]);
  }
  return Math.abs(area / 2);
}
// only for the demo
(function(){
  document.getElementById('number_of_points').addEventListener('change', function(){
    var svg = document.getElementById("svg");
    var bezier_points = getBezierPathPoints(svg, "path");
    // in this example there is only one bezier curve
    bezier_points = bezier_points[0];
    // number of approximation points
    var approx_points_num = parseInt(this.value);
    var approx_points = getBezierApproxPoints(bezier_points, approx_points_num);
    var doc = svg.ownerDocument;
    // remove polygon
    var polygons;
    while((polygons = doc.getElementsByTagName("polygon")).length > 0){
      polygons[0].parentNode.removeChild(polygons[0]);
    }
    // remove old circles
    var circles;
    while((circles = doc.getElementsByTagName("circle")).length > 0){
      circles[0].parentNode.removeChild(circles[0]);
    }
    // add new circles and create polygon
    var polygon_points = [];
    for(var i = 0; i < approx_points.length; i++){
      let circle = doc.createElementNS('http://www.w3.org/2000/svg', 'circle');
      circle.setAttribute('cx', approx_points[i][0]);
      circle.setAttribute('cy', approx_points[i][1]);
      circle.setAttribute('r', 1);
      circle.setAttribute('fill', '#449944');
      svg.appendChild(circle);
      polygon_points.push(approx_points[i][0], approx_points[i][1]);
    }
    var polygon = doc.createElementNS('http://www.w3.org/2000/svg', 'polygon');
    polygon.setAttribute("points", polygon_points.join(" "));
    polygon.setAttribute("stroke", "transparent");
    polygon.setAttribute("fill", "#cccc00");
    polygon.setAttribute("opacity", "0.7");
    svg.appendChild(polygon);
    doc.querySelector("output[name='points']").innerHTML = approx_points_num;
    doc.querySelector("output[name='area']").innerHTML = polyArea(approx_points);
  });
  var event = new Event("change");
  document.getElementById("number_of_points").dispatchEvent(event);
})();

<html>
  <body>
    <div style="width: 100%; text-align: center;">
      <svg width="250px" height="120px" viewBox="-5 -5 45 30" id="svg">
        <path d="M 0 0 C 10 15 50 40 30 0 Z" fill="transparent" stroke="black" id="path" />
      </svg>
      <br />
      <input type="range" min="3" max="100" value="5" class="slider" id="number_of_points">
      <br />
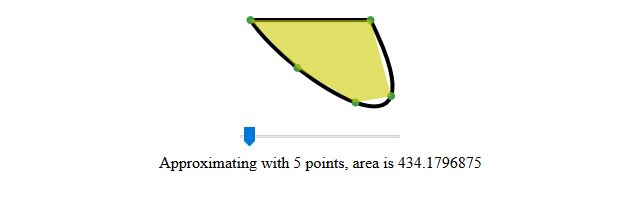
      Approximating with 
      <output name="points" for="number_of_points"></output>
      points, area is
      <output name="area"></output>
    </div>
  </body>
</html>

Solution 4

Firstly, I am not so familiar with Bézier curves, but I know that they are continuous functions. If you ensure that your cubic curve does not intersect itself, you may integrate it in closed form (I mean by using analytic integrals) on the given enclosing domain ([a-b]) and subtract the area of triangle that is formed by the the end joining straight line and the X axis. In case of intersection with the Bézier curve and end joining straight line, you may divide into sections and try to calculate each area separately in a consistent manner..

For me suitable search terms are "continuous function integration" "integrals" "area under a function" "calculus"

Of course you may generate discrete data from your Bézier curve fn and obtain discrete X-Y data and calculate the integral approximately.

Solution 5

I like the solution in the accepted answer by Phrogz, but I also looked a little further and found a way to do the same with Paper.js using the CompoundPath class and area property. See my Paper.js demo.

The result (surface area = 11856) is the exact same as with Phrogz's demo when using threshold 0, but the processing seems a lot quicker! I know it's overkill to load Paper.js just to calculate the surface area, but if you are considering implementing a framework or feel like investigating how Paper.js does it...

View more solutions

10,840

Author by

MikeW

Updated on June 04, 2022

Comments

MikeW 6 months

Given the following path (for example) which describes a SVG cubic bezier curve: "M300,140C300,40,500,40,500,140", and assuming a straight line connecting the end points 300,140 to 500,140 (closing the area under the curve), is it possible to calculate the area so enclosed?

Can anyone suggest a formula (or JavaScript) to accomplish this?
Semih Ozmen over 10 years

actually your solution is innovative, of course it has no chance against to closed form solutions but you may write an optimized code and compare with a solution by numerical integration methods which follows similar approach with yours.
MikeW over 10 years

This solution is quite adequate for my purposes AND it saved me from revisiting college calculus! I had already written a function to calculate the area of polygons. I wish it had occurred to me to convert the curves; it seems obvious now. Thank you to @Phrogz...
MikeW over 10 years

Phrogz demo (and the source from the demo) lays out a simple and elegant solution to this question. Basically you convert the curve (ANY type of curve or arc) to a polygon that approximates the curve. Then it's a fairly trivial matter to calculate the area of the polygon. This is particularly useful since by extension you can calculate the area of any svg path (at least a reasonable approximation).
Timo Kähkönen over 9 years

This is a fine quick and dirty brute force solution. But if you want more exact precision, this is not suitable: try to set extra samples to 100 and make a tight curve (curve that has a high curvature area somewhere). You see that in this part there are not enough samples. The solution is then to increase the sample size from 100 to 200 or 500, but this makes the code slow when there are tens of curves. Better, faster and more precise solution is eg. an adaptive curve splitting, that produces more samples on tight parts and less in looser parts of the curve.
Phrogz almost 9 years

@Timo OK, you've convinced me. I've edited my answer with a new function that adaptively subdivides a <path> to produce a poly. Note that this new technique may fail for certain self-crossing paths. (Unlucky sample placement resulting in a self-crossing polygon can result in near-zero area, causing the subdivision algorithm to consider its work done.)
RamenChef almost 4 years

I followed your link and it went through a whole bunch of redirects to a place to buy a watch. I'm not sure if it's working right.
miile7 over 3 years

According to Mozilla the SVGPathElement.getPointAtLength() is deprecated. In addition this only works in javascript if there is the SVGPathElement.getPointAtLength() function. I needed it in the back end where I cannot use this method. For more details have a look at my answer below.
Robert Longson over 3 years

deprecated is rather misleading, it's simply moved to the parent interface so you can keep using it without worrying. The note below the deprecation explains that.
R4444 over 3 years

Please add some description instead of putting just the code
Admin over 3 years

Short description is contained inside the code I put, but you are right, it's not complete. I'll try to post longer explanation, but it will take some time.
Admin over 3 years

Please, also try to run this code on web browser, it will clarify the idea.
BallpointBen almost 2 years

The bit of magic that actually calculates the area, area += (p2.x+p1.x) * (p2.y-p1.y), is known as the shoelace formula: en.wikipedia.org/wiki/Shoelace_formula
Armen Michaeli over 1 year

Sorry for digging up an old answer, but in my understanding, the difficult part here is representing the curve as a y = f(x) function to compute the integral of. A Bézier curve is typically represented by a duo of parametric functions x = X(t) and y = Y(t), which at least in my understanding again, does not lend itself well to computing a definite integral that amounts to the area confined inside your drawn red and green segments. So while technically you're right about what you wrote, the challenge here is to compute the y = f(x) in the first place.
ashleedawg over 1 year

I don't know about before but getPointAtLength is not deprecated now. Regardless, the demo is broken, sadly, as I noted in an edit to the answer. (Yet another case for keeping things like demo's limited to internal Snippets, attached to the answer.)
ashleedawg over 1 year

@nbonneel - "Copying the text in case the website goes down..." ...Thank you! The website did indeed go down. I wish everyone would take the extra second when sharing external info! In this case there is an archived of the page, but formatting is messed up, and not all pages get archived... Anyway, this was the info I've been seeking, thanks again!
kamae about 1 year

I think this is the best answer. This is not an approximation.
Chiara Ani about 1 year

Your answer is useful for polygons but not for curves.
Admin about 1 year

If applied properly, it can work. In my case, I made 1000 points from the curve in excel by varying T.