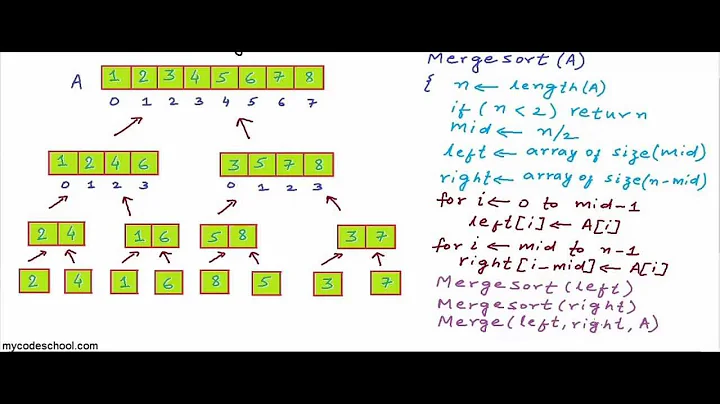
How to sort in-place using the merge sort algorithm?

Question

I know the question is not too specific.

All I want is someone to tell me how to convert a normal merge sort into an in-place merge sort (or a merge sort with constant extra space overhead).

All I can find (on the net) is pages saying "it is too complex" or "out of scope of this text".

The only known ways to merge in-place (without any extra space) are too complex to be reduced to practical program. (taken from here)

Even if it is too complex, what is the basic concept of how to make the merge sort in-place?

Solution 1

Knuth left this as an exercise (Vol 3, 5.2.5). There do exist in-place merge sorts. They must be implemented carefully.

First, naive in-place merge such as described here isn't the right solution. It downgrades the performance to O(N²).

The idea is to sort part of the array while using the rest as working area for merging.

For example like the following merge function.

void wmerge(Key* xs, int i, int m, int j, int n, int w) {
    while (i < m && j < n)
        swap(xs, w++, xs[i] < xs[j] ? i++ : j++);
    while (i < m)
        swap(xs, w++, i++);
    while (j < n)
        swap(xs, w++, j++);
}  

It takes the array xs, the two sorted sub-arrays are represented as ranges [i, m) and [j, n) respectively. The working area starts from w. Compare with the standard merge algorithm given in most textbooks, this one exchanges the contents between the sorted sub-array and the working area. As the result, the previous working area contains the merged sorted elements, while the previous elements stored in the working area are moved to the two sub-arrays.

However, there are two constraints that must be satisfied:

1. The work area should be within the bounds of the array. In other words, it should be big enough to hold elements exchanged in without causing any out-of-bound error.
2. The work area can be overlapped with either of the two sorted arrays; however, it must ensure that none of the unmerged elements are overwritten.

With this merging algorithm defined, it's easy to imagine a solution, which can sort half of the array; The next question is, how to deal with the rest of the unsorted part stored in work area as shown below:

... unsorted 1/2 array ... | ... sorted 1/2 array ...

One intuitive idea is to recursive sort another half of the working area, thus there are only 1/4 elements haven't been sorted yet.

... unsorted 1/4 array ... | sorted 1/4 array B | sorted 1/2 array A ...

The key point at this stage is that we must merge the sorted 1/4 elements B with the sorted 1/2 elements A sooner or later.

Is the working area left, which only holds 1/4 elements, big enough to merge A and B? Unfortunately, it isn't.

However, the second constraint mentioned above gives us a hint, that we can exploit it by arranging the working area to overlap with either sub-array if we can ensure the merging sequence that the unmerged elements won't be overwritten.

Actually, instead of sorting the second half of the working area, we can sort the first half, and put the working area between the two sorted arrays like this:

... sorted 1/4 array B | unsorted work area | ... sorted 1/2 array A ...

This setup effectively arranges the work area overlap with the sub-array A. This idea is proposed in [Jyrki Katajainen, Tomi Pasanen, Jukka Teuhola. ``Practical in-place mergesort''. Nordic Journal of Computing, 1996].

So the only thing left is to repeat the above step, which reduces the working area from 1/2, 1/4, 1/8, … When the working area becomes small enough (for example, only two elements left), we can switch to a trivial insertion sort to end this algorithm.

Here is the implementation in ANSI C based on this paper.

void imsort(Key* xs, int l, int u);

void swap(Key* xs, int i, int j) {
    Key tmp = xs[i]; xs[i] = xs[j]; xs[j] = tmp;
}

/* 
 * sort xs[l, u), and put result to working area w. 
 * constraint, len(w) == u - l
 */
void wsort(Key* xs, int l, int u, int w) {
    int m;
    if (u - l > 1) {
        m = l + (u - l) / 2;
        imsort(xs, l, m);
        imsort(xs, m, u);
        wmerge(xs, l, m, m, u, w);
    }
    else
        while (l < u)
            swap(xs, l++, w++);
}

void imsort(Key* xs, int l, int u) {
    int m, n, w;
    if (u - l > 1) {
        m = l + (u - l) / 2;
        w = l + u - m;
        wsort(xs, l, m, w); /* the last half contains sorted elements */
        while (w - l > 2) {
            n = w;
            w = l + (n - l + 1) / 2;
            wsort(xs, w, n, l);  /* the first half of the previous working area contains sorted elements */
            wmerge(xs, l, l + n - w, n, u, w);
        }
        for (n = w; n > l; --n) /*switch to insertion sort*/
            for (m = n; m < u && xs[m] < xs[m-1]; ++m)
                swap(xs, m, m - 1);
    }
}

Where wmerge is defined previously.

The full source code can be found here and the detailed explanation can be found here

By the way, this version isn't the fastest merge sort because it needs more swap operations. According to my test, it's faster than the standard version, which allocates extra spaces in every recursion. But it's slower than the optimized version, which doubles the original array in advance and uses it for further merging.

Solution 2

Including its "big result", this paper describes a couple of variants of in-place merge sort (PDF):

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.22.5514&rep=rep1&type=pdf

In-place sorting with fewer moves

Jyrki Katajainen, Tomi A. Pasanen

It is shown that an array of n elements can be sorted using O(1) extra space, O(n log n / log log n) element moves, and n log₂n + O(n log log n) comparisons. This is the first in-place sorting algorithm requiring o(n log n) moves in the worst case while guaranteeing O(n log n) comparisons, but due to the constant factors involved the algorithm is predominantly of theoretical interest.

I think this is relevant too. I have a printout of it lying around, passed on to me by a colleague, but I haven't read it. It seems to cover basic theory, but I'm not familiar enough with the topic to judge how comprehensively:

http://comjnl.oxfordjournals.org/cgi/content/abstract/38/8/681

Optimal Stable Merging

Antonios Symvonis

This paper shows how to stably merge two sequences A and B of sizes m and n, m ≤ n, respectively, with O(m+n) assignments, O(mlog(n/m+1)) comparisons and using only a constant amount of additional space. This result matches all known lower bounds...

Solution 3

It really isn't easy or efficient, and I suggest you don't do it unless you really have to (and you probably don't have to unless this is homework since the applications of inplace merging are mostly theoretical). Can't you use quicksort instead? Quicksort will be faster anyway with a few simpler optimizations and its extra memory is O(log N).

Anyway, if you must do it then you must. Here's what I found: one and two. I'm not familiar with the inplace merge sort, but it seems like the basic idea is to use rotations to facilitate merging two arrays without using extra memory.

Note that this is slower even than the classic merge sort that's not inplace.

Solution 4

The critical step is getting the merge itself to be in-place. It's not as difficult as those sources make out, but you lose something when you try.

Looking at one step of the merge:

[...list-sorted...|x...list-A...|y...list-B...]

We know that the sorted sequence is less than everything else, that x is less than everything else in A, and that y is less than everything else in B. In the case where x is less than or equal to y, you just move your pointer to the start of A on one. In the case where y is less than x, you've got to shuffle y past the whole of A to sorted. That last step is what makes this expensive (except in degenerate cases).

It's generally cheaper (especially when the arrays only actually contain single words per element, e.g., a pointer to a string or structure) to trade off some space for time and have a separate temporary array that you sort back and forth between.

Solution 5

This answer has a code example, which implements the algorithm described in the paper Practical In-Place Merging by Bing-Chao Huang and Michael A. Langston. I have to admit that I do not understand the details, but the given complexity of the merge step is O(n).

From a practical perspective, there is evidence that pure in-place implementations are not performing better in real world scenarios. For example, the C++ standard defines std::inplace_merge, which is as the name implies an in-place merge operation.

Assuming that C++ libraries are typically very well optimized, it is interesting to see how it is implemented:

1) libstdc++ (part of the GCC code base): std::inplace_merge

The implementation delegates to __inplace_merge, which dodges the problem by trying to allocate a temporary buffer:

typedef _Temporary_buffer<_BidirectionalIterator, _ValueType> _TmpBuf;
_TmpBuf __buf(__first, __len1 + __len2);

if (__buf.begin() == 0)
  std::__merge_without_buffer
    (__first, __middle, __last, __len1, __len2, __comp);
else
  std::__merge_adaptive
   (__first, __middle, __last, __len1, __len2, __buf.begin(),
     _DistanceType(__buf.size()), __comp);

Otherwise, it falls back to an implementation (__merge_without_buffer), which requires no extra memory, but no longer runs in O(n) time.

2) libc++ (part of the Clang code base): std::inplace_merge

Looks similar. It delegates to a function, which also tries to allocate a buffer. Depending on whether it got enough elements, it will choose the implementation. The constant-memory fallback function is called __buffered_inplace_merge.

Maybe even the fallback is still O(n) time, but the point is that they do not use the implementation if temporary memory is available.

---

Note that the C++ standard explicitly gives implementations the freedom to choose this approach by lowering the required complexity from O(n) to O(N log N):

Complexity: Exactly N-1 comparisons if enough additional memory is available. If the memory is insufficient, O(N log N) comparisons.

Of course, this cannot be taken as a proof that constant space in-place merges in O(n) time should never be used. On the other hand, if it would be faster, the optimized C++ libraries would probably switch to that type of implementation.

View more solutions

Comments

[Chris Lercher]

Nice question, I asked that myself when reading through a question from yesterday: stackoverflow.com/questions/2566459/…

[Thomas Mueller]

Just for reference, here is a nice implementation of a stable in-place merge sort. Complicated, but not too bad. I ended up implementing both a stable in-place merge sort and a stable in-place quicksort in Java. Please note the complexity is O(n (log n)^2)

[Branko Dimitrijevic]

There is a fairly simple method described here: xinok.wordpress.com/2014/08/17/…

[Paul]

In the usual split and merge algorithm, if you define the pointer array to be a linked list L(i) where you have an entry address that is the address of the first record in sorted order, and the pointer at that address is the address of the 2nd record in sorted order, and so forth, you will find that you CAN merge two linked -lists "in place" in O(n) You end up with a separate pointer as the entry point to the linked list and a linked list of n-1 pointers. I set the nth linked list entry to zero as a STOP indicator, which is useful in merging. You recur through the results using i=L(i)

[Donal Fellows]

Quicksort isn't stable. That really matters for a lot of production code.

[jk.]

quicksort can be stable, and iirc merge sort is not necessarily stable if in place

[HoboBen]

Quicksort also has a O(n^2) worst case for specially crafted input

[valyala]

Your in-place merge has O(m*n) worst-case complexity, where m is A size, and n is B size. This is the case when the first item in A is larger than the last item in B. The complexity can be improved to O(k*log(k)+m+n), where k=min(m,n) by adding a heap between A and B. This heap should contain items from A, which are larger the remaining items in B, but smaller than the remaining items in A. If A is exhausted first, then the heap must be moved to the end of B. Otherwise the heap must be moved to the beginning of A. Then heap items must be popped out in-place and reversed to complete the merge.

[user541686]

In-place merging is practically useful in C++ (at least before C++11): some objects are swappable but not copyable!

[martinkunev]

Note that this implementation takes Θ(n^2 log n) time in the worst case (reversed array).

[Thomas Ahle]

Did you write this? How does it overcome the difficulties expressed in the other answers? What is its running time?

[Johnny Cage]

This is adapted from my own custom library, but I didn't create these algorithms if that's what you're asking. Growth is O(n (log n)^2) without auxiliary memory; O(n log n) with full buffer. This tries to be a practical implementation, and is structured to show constituent algorithms.

[Larry LIU Xinyu]

I removed the link for that chapter. The content can be found in chapter 13 of the book: sites.google.com/site/algoxy/home/elementary-algorithms.pdf

[martinkunev]

@valyala Note that when using a heap, the sort is no longer stable. Also, if you use a heap, you can go with heap sort instead of merge sort.

[jack]

Why do you need recursion or extra buffer to merge two sorted lists? I think it can be done by moving the two pointers forward and swapping if left is bigger than right.

[greybeard]

Knuth left this as an exercise (Vol 3, 5.2.5). refers to ex. 13.[40] Implement the internal sorting method suggested [at the close of this section], producing which sorts random data in O(N) units of time mith only O(sqrt(N)) additional memory locations.? (40 indicating Quite a difficult or lengthy problem which is perhaps suitable as a term project in classroom situations.)

[code4fun]

I think that the time-complexity of in-place algorithm mentioned in the penguin.ew site is O(log n * n^2).Since we have log n merges and each merge is of the order O(n ^2).Isnt that right ?

[Paul Stelian]

Is this algorithm still stable and in n log n time?

[rcgldr]

@PaulStelian - it's not stable. Elements in the working area are rearranged according to the ordering operations on elements in the sorted area. This means working area elements with equal values will get rearranged so they are no longer in their original order.

[Paul Stelian]

@rcgldr Okay, so it isn't of that much interest anymore. I am aware of the Block Merge Sort algorithm which is stable though.

[glaba]

It's both O(n^2) and also highly unreadable (because of the occasional syntax errors and inconsistent / poor style)

[rcgldr]

@PaulStelian - Wiki has an article for block merge sort, which as you commented is stable. It works best if there are at least 2 · sqrt(n) unique values, which allows them to be re-ordered to provide working areas of an array and remain stable.

[kristianp]

Is Quicksort's extra memory really O(log n)? I thought being an in-place algorithm it would be O(1) extra memory? Oh, being recursive, the stack usage is O(log n).

[greybeard]

Outside web archives, Jason Harrison's In-Place Merge Sort (two) is featured, for one place, in this collection of sort implementations, apparently started by the man himself. Several are not properly converted to HTML while labelled thus (use view source).

[SpawN]

Best Case of inplace merge Algorithm in mergeSort ? When array is already sorted can we say O(m) ? where m is the size of the 1st sorted array that is one of the inputs to merge algo.

[LMD]

@kristianp: Quicksort's extra memory depends on how you manage your recursion stack. If managed cleverly, it can be shown to never exceed O(log n); a naive recursive implementation will likely use O(n) memory in the worst case though.

[user202729]

Just want to note that in-place merge is possible in optimal asymptotic time complexity, see c++ - Is it possible to do an inplace merge without temporary storage? - Stack Overflow

[SJHowe]

What working area? This is theoretical and does not mean anything. If you are inplace merging, say 20,000 elements with 20,000 elements, that is 40,000 elements a 1/4 is 10,0000 elements. But those areas are occupied and cannot be unoccupied. The reality is even without a buffer, at least 1 element is on the stack and via rotation and shifts (a lot of them) the elements are put in place. All the various truly inplace algorithms are using that 1 element to effect an inplace merge