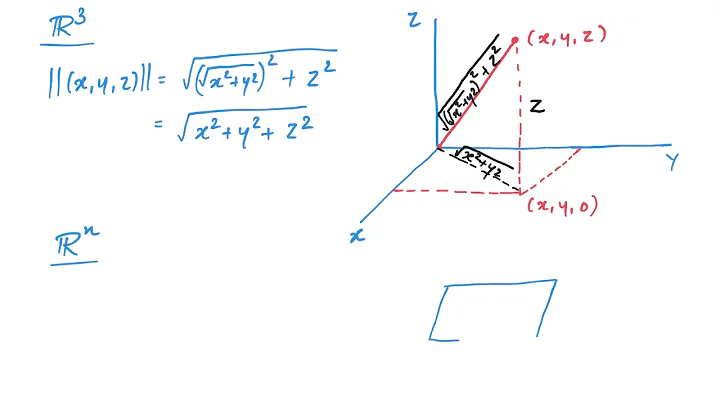
Is "norm" equivalent to "Euclidean distance"?

Question

I am not sure whether "norm" and "Euclidean distance" mean the same thing. Please could you help me with this distinction.

I have an n by m array a, where m > 3. I want to calculate the Eculidean distance between the second data point a[1,:] to all the other points (including itself). So I used the np.linalg.norm, which outputs the norm of two given points. But I don't know if this is the right way of getting the EDs.

import numpy as np

a = np.array([[0, 0, 0 ,0 ], [1, 1 , 1, 1],[2,2, 2, 3], [3,5, 1, 5]])
N = a.shape[0] # number of row
pos = a[1,:] # pick out the second data point. 
dist = np.zeros((N,1), dtype=np.float64)

for i in range(N):
    dist[i]= np.linalg.norm(a[i,:] - pos)

Solution 1

A norm is a function that takes a vector as an input and returns a scalar value that can be interpreted as the "size", "length" or "magnitude" of that vector. More formally, norms are defined as having the following mathematical properties:

• They scale multiplicatively, i.e. Norm(a·v) = |a|·Norm(v) for any scalar a
• They satisfy the triangle inequality, i.e. Norm(u + v) ≤ Norm(u) + Norm(v)
• The norm of a vector is zero if and only if it is the zero vector, i.e. Norm(v) = 0 ⇔ v = 0

The Euclidean norm (also known as the L² norm) is just one of many different norms - there is also the max norm, the Manhattan norm etc. The L² norm of a single vector is equivalent to the Euclidean distance from that point to the origin, and the L² norm of the difference between two vectors is equivalent to the Euclidean distance between the two points.

---

As @nobar's answer says, np.linalg.norm(x - y, ord=2) (or just np.linalg.norm(x - y)) will give you Euclidean distance between the vectors x and y.

Since you want to compute the Euclidean distance between a[1, :] and every other row in a, you could do this a lot faster by eliminating the for loop and broadcasting over the rows of a:

dist = np.linalg.norm(a[1:2] - a, axis=1)

It's also easy to compute the Euclidean distance yourself using broadcasting:

dist = np.sqrt(((a[1:2] - a) ** 2).sum(1))

The fastest method is probably scipy.spatial.distance.cdist:

from scipy.spatial.distance import cdist

dist = cdist(a[1:2], a)[0]

---

Some timings for a (1000, 1000) array:

a = np.random.randn(1000, 1000)

%timeit np.linalg.norm(a[1:2] - a, axis=1)
# 100 loops, best of 3: 5.43 ms per loop

%timeit np.sqrt(((a[1:2] - a) ** 2).sum(1))
# 100 loops, best of 3: 5.5 ms per loop

%timeit cdist(a[1:2], a)[0]
# 1000 loops, best of 3: 1.38 ms per loop

# check that all 3 methods return the same result
d1 = np.linalg.norm(a[1:2] - a, axis=1)
d2 = np.sqrt(((a[1:2] - a) ** 2).sum(1))
d3 = cdist(a[1:2], a)[0]

assert np.allclose(d1, d2) and np.allclose(d1, d3)

Solution 2

The concept of a "norm" is a generalized idea in mathematics which, when applied to vectors (or vector differences), broadly represents some measure of length. There are various different approaches to computing a norm, but the one called Euclidean distance is called the "2-norm" and is based on applying an exponent of 2 (the "square"), and after summing applying an exponent of 1/2 (the "square root").

---

It's a bit cryptic in the docs, but you get Euclidean distance between two vectors by setting the parameter ord=2.

sum(abs(x)**ord)**(1./ord)

becomes sqrt(sum(x**2)).

Note: as pointed out by @Holt, the default value is ord=None, which is documented to compute the "2-norm" for vectors. This is, therefore, equivalent to ord=2 (Euclidean distance).

Comments

[Holt]

You also get it with the default None value.

[Brent Bradburn]

@Holt: Thanks, I didn't notice that. The default is None which computes the "2-norm", presumably matching ord=2.

[Brent Bradburn]

Seems a shame to have all this discussion of the "2-norm" without mentioning it's most famous form: The Pythagorean theorem.