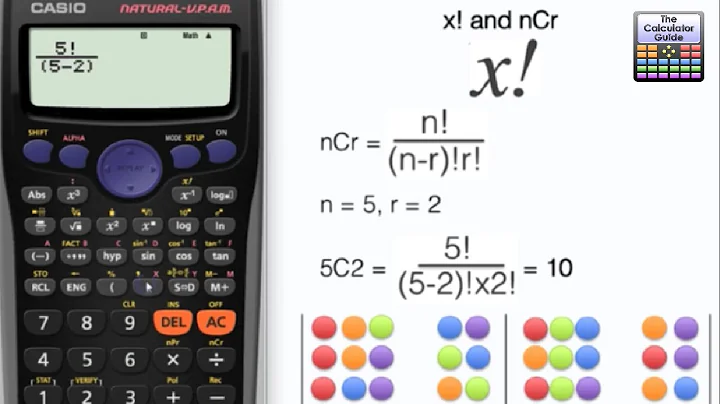Which is better way to calculate nCr

Question

Approach 1:
C(n,r) = n!/(n-r)!r!

Approach 2:
In the book Combinatorial Algorithms by wilf, i have found this:
C(n,r) can be written as C(n-1,r) + C(n-1,r-1).

e.g.

C(7,4) = C(6,4) + C(6,3) 
       = C(5,4) + C(5,3) + C(5,3) + C(5,2)
       .   .
       .   .
       .   .
       .   .
       After solving
       = C(4,4) + C(4,1) + 3*C(3,3) + 3*C(3,1) + 6*C(2,1) + 6*C(2,2)

As you can see, the final solution doesn't need any multiplication. In every form C(n,r), either n==r or r==1.

Here is the sample code i have implemented:

int foo(int n,int r)
{
     if(n==r) return 1;
     if(r==1) return n;
     return foo(n-1,r) + foo(n-1,r-1);
}

See output here.

In the approach 2, there are overlapping sub-problems where we are calling recursion to solve the same sub-problems again. We can avoid it by using Dynamic Programming.

I want to know which is the better way to calculate C(n,r)?.

Solution 1

Both approaches will save time, but the first one is very prone to integer overflow.

Approach 1:

This approach will generate result in shortest time (in at most n/2 iterations), and the possibility of overflow can be reduced by doing the multiplications carefully:

long long C(int n, int r) {
    if(r > n - r) r = n - r; // because C(n, r) == C(n, n - r)
    long long ans = 1;
    int i;

    for(i = 1; i <= r; i++) {
        ans *= n - r + i;
        ans /= i;
    }

    return ans;
}

This code will start multiplication of the numerator from the smaller end, and as the product of any k consecutive integers is divisible by k!, there will be no divisibility problem. But the possibility of overflow is still there, another useful trick may be dividing n - r + i and i by their GCD before doing the multiplication and division (and still overflow may occur).

Approach 2:

In this approach, you'll be actually building up the Pascal's Triangle. The dynamic approach is much faster than the recursive one (the first one is O(n^2) while the other is exponential). However, you'll need to use O(n^2) memory too.

# define MAX 100 // assuming we need first 100 rows
long long triangle[MAX + 1][MAX + 1];

void makeTriangle() {
    int i, j;

    // initialize the first row
    triangle[0][0] = 1; // C(0, 0) = 1

    for(i = 1; i < MAX; i++) {
        triangle[i][0] = 1; // C(i, 0) = 1
        for(j = 1; j <= i; j++) {
            triangle[i][j] = triangle[i - 1][j - 1] + triangle[i - 1][j];
        }
    }
}

long long C(int n, int r) {
    return triangle[n][r];
}

Then you can look up any C(n, r) in O(1) time.

If you need a particular C(n, r) (i.e. the full triangle is not needed), then the memory consumption can be made O(n) by overwriting the same row of the triangle, top to bottom.

# define MAX 100
long long row[MAX + 1];

int C(int n, int r) {
    int i, j;

    // initialize by the first row
    row[0] = 1; // this is the value of C(0, 0)

    for(i = 1; i <= n; i++) {
        for(j = i; j > 0; j--) {
             // from the recurrence C(n, r) = C(n - 1, r - 1) + C(n - 1, r)
             row[j] += row[j - 1];
        }
    }

    return row[r];
}

The inner loop is started from the end to simplify the calculations. If you start it from index 0, you'll need another variable to store the value being overwritten.

Solution 2

I think your recursive approach should work efficiently with DP. But it will start giving problems once the constraints increase. See http://www.spoj.pl/problems/MARBLES/

Here is the function which i use in online judges and coding contests. So it works quite fast.

long combi(int n,int k)
{
    long ans=1;
    k=k>n-k?n-k:k;
    int j=1;
    for(;j<=k;j++,n--)
    {
        if(n%j==0)
        {
            ans*=n/j;
        }else
        if(ans%j==0)
        {
            ans=ans/j*n;
        }else
        {
            ans=(ans*n)/j;
        }
    }
    return ans;
}

It is an efficient implementation for your Approach #1

Solution 3

Your Recursive Approach is fine but using DP with your approach will reduce the overhead of solving subproblems again.Now since we already have two Conditions-

nCr(n,r) = nCr(n-1,r-1) + nCr(n-1,r);

nCr(n,0)=nCr(n,n)=1;

Now we can easily build a DP solution by storing our subresults in a 2-D array-

int dp[max][max];
//Initialise array elements with zero
int nCr(int n, int r)
{
       if(n==r) return dp[n][r] = 1; //Base Case
       if(r==0) return dp[n][r] = 1; //Base Case
       if(r==1) return dp[n][r] = n;
       if(dp[n][r]) return dp[n][r]; // Using Subproblem Result
       return dp[n][r] = nCr(n-1,r) + nCr(n-1,r-1);
}

Now if you want to further otimise, Getting the prime factorization of the binomial coefficient is probably the most efficient way to calculate it, especially if multiplication is expensive.

The fastest method I know is Vladimir's method. One avoids division all together by decomposing nCr into prime factors. As Vladimir says you can do this pretty efficiently using Eratosthenes sieve.Also,Use Fermat's little theorem to calculate nCr mod MOD(Where MOD is a prime number).

Comments

[Admin]

if(r==1) return n; are you sure you don't want to return 1 instead?

[ypercubeᵀᴹ]

See this question: counting combinations and permutations efficiently

[Ben Voigt]

Also stackoverflow.com/a/9331125/103167

[kapil]

add the case if(r==0) return 1 ; or else the code gives segmentation fault on nc0

[Tushar Jain]

May I know , what is complexcity of this algorithm?

[Daniel Fischer]

If you factor out the gcd of i and n-r+i, you can divide first and multiply thereafter. Then you only have overflow if the result overflows.

[Ankesh Anand]

Do you really need those 3 conditions? I guess the third condition ans=(ans*n)/j; is sufficient for every iteration. And I fail to understand how your method prevents integer overflow. ans*n can very well go out of bounds.

[nims]

@AnkeshAnand True ans=(ans*n)/j can go out of bounds, but the first two conditions are for those cases where we can prevent overflow by performing a division first. They are just an attempt to compute for those very few cases which just ans=(ans*n)/j won't be able to compute due to overflow.

[Ankesh Anand]

I get it, I think if the problem constraints are very large, then (ans*n) will go out of bounds irrespective of your first two checks. I am using the last condition currently, and it works, on a large set of problems.

[toothie]

Could you please explain approach 1 a little more? I am unable to understand the part where 'a' is multiplied by 'n - r + i' and is divided by 'i'

[Sufian Latif]

@toothie It comes from the formula: C(n, r) = n (n - 1) ... (n - r + i) ... (n - r + 1) / 1.2. ... .i. ... r can be re-written as C(n, r) = (n / r) ((n - 1) / (r - 1)) ... ((n - r + i) / i) ... ((n - r + 1) / 1). The first approach multiplies them from the last.

[toothie]

@0605002 Oh. Got it now. Thanks

[sathya_dev]

@0605002 . I'm not getting why the outer loop is like i<n instead of i<=n .If I'm not wrong after each i'th iteration row[j] will be equivalent to iCr. Please clarify if I'm wrong. Thanks

[Peter Cordes]

The error from doing ans *= n/j without checking first is (ans*n)%j. Can we come up with a way to calculate that without overflow, so we can always avoid overflow of temporary results? Hopefully with only a couple divisions, because they're slow and usually barely pipelined.

[Suraj Jain]

it is wrong for 63C29. CORRECT IS: 759510004936100355

[Job]

Is this the Vladimir's Method you speak of? Is this the only version of it? quora.com/What-are-some-efficient-algorithms-to-compute-nCr

[ajaysinghnegi]

To calculate ncr%m, Can I just do return dp[n][r] = (nCr(n-1,r)%m + nCr(n-1,r-1)%m)%m;