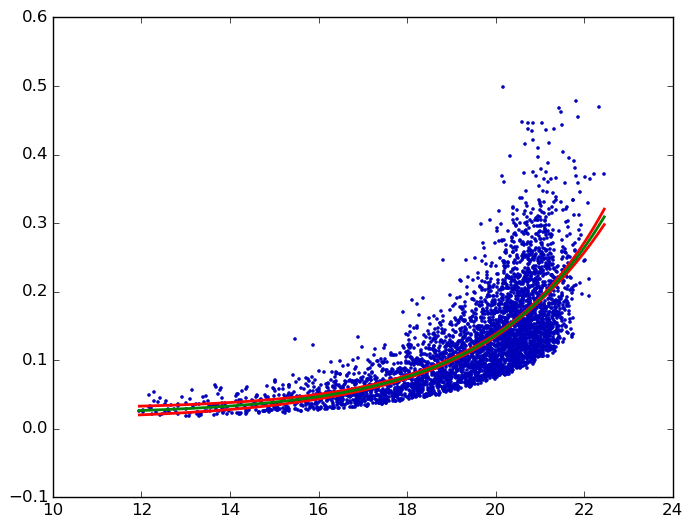
Confidence interval for exponential curve fit
Solution 1
Gabriel's answer is incorrect. Here in red the 95% confidence band for his data as calculated by GraphPad Prism:
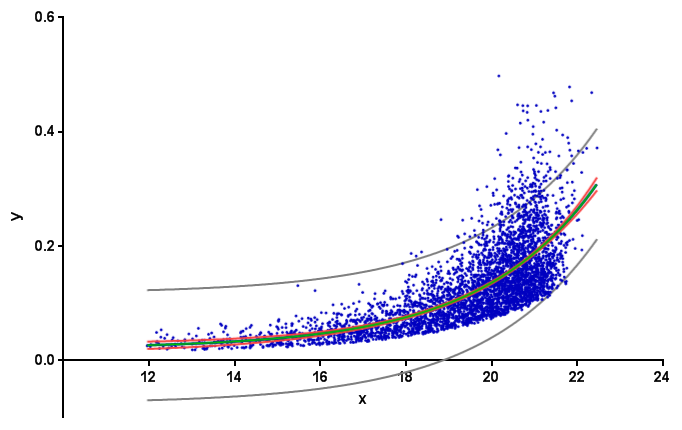
Background: the "confidence interval of a fitted curve" is typically called confidence band. For a 95% confidence band, one can be 95% confident that it contains the true curve. (This is different from prediction bands, shown above in gray. Prediction bands are about future data points. For more details, see, e.g., this page of the GraphPad Curve Fitting Guide.)
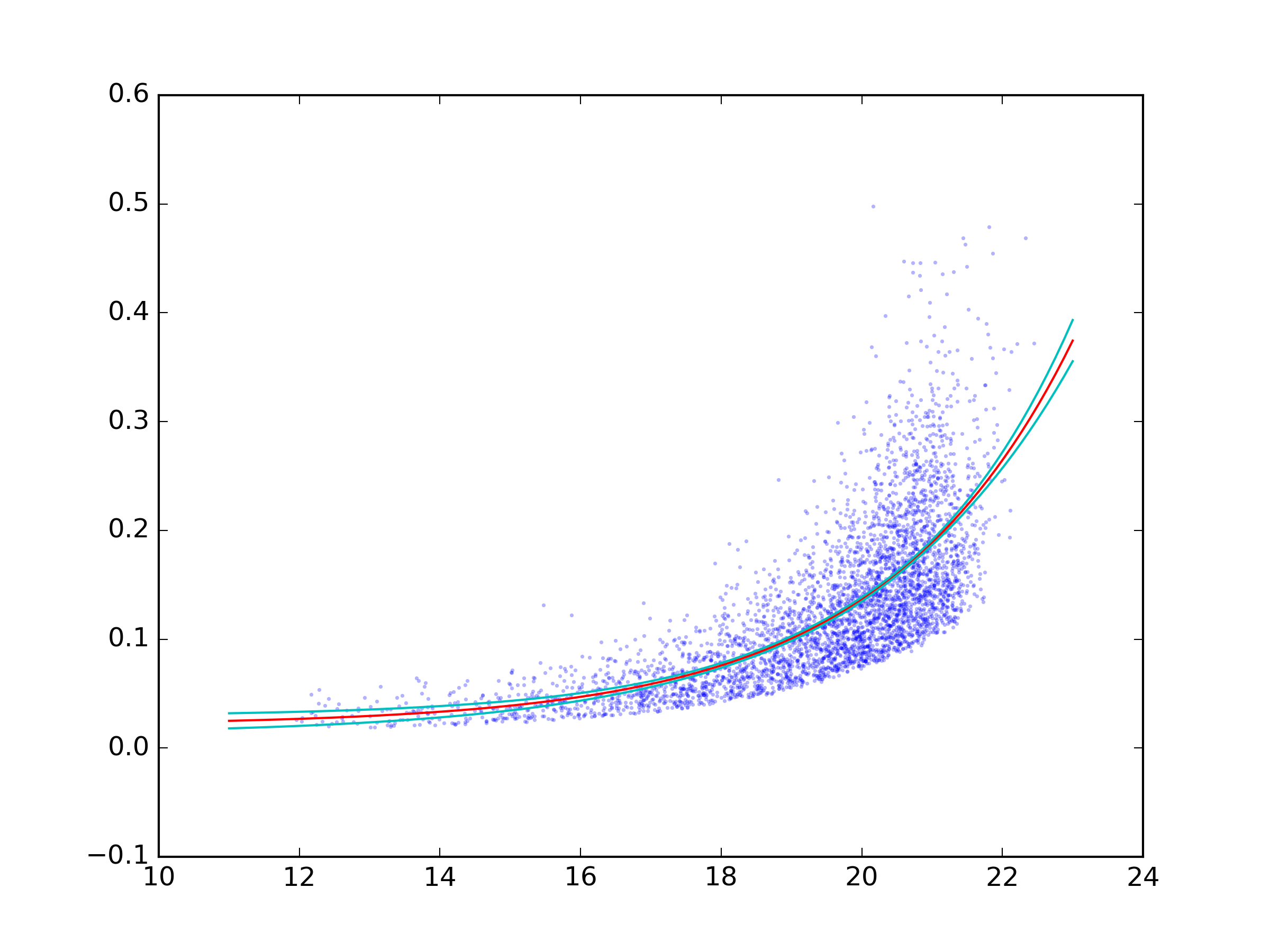
In Python, kmpfit can calculate the confidence band for non-linear least squares. Here for Gabriel's example:
from pylab import *
from kapteyn import kmpfit
x, y = np.loadtxt('_exp_fit.txt', unpack=True)
def model(p, x):
a, b, c = p
return a*np.exp(b*x)+c
f = kmpfit.simplefit(model, [.1, .1, .1], x, y)
print f.params
# confidence band
a, b, c = f.params
dfdp = [np.exp(b*x), a*x*np.exp(b*x), 1]
yhat, upper, lower = f.confidence_band(x, dfdp, 0.95, model)
scatter(x, y, marker='.', s=10, color='#0000ba')
ix = np.argsort(x)
for i, l in enumerate((upper, lower, yhat)):
plot(x[ix], l[ix], c='g' if i == 2 else 'r', lw=2)
show()
The dfdp are the partial derivatives ∂f/∂p of the model f = a*e^(b*x) + c with respect to each parameter p (i.e., a, b, and c). For background, see the kmpfit Tutorial or this page of the GraphPad Curve Fitting Guide. (Unlike my sample code, the kmpfit Tutorial does not use confidence_band() from the library but its own, slightly different, implementation.)
Finally, the Python plot matches the Prism one:
Solution 2
You can use the uncertainties module to do the uncertainty calculations.
uncertainties keeps track of uncertainties and correlation. You can create correlated uncertainties.ufloat directly from the output of curve_fit.
To be able to do those calculation on non-builtin operations such as exp you need to use the functions from uncertainties.unumpy.
You should also avoid your from pylab import * import. This even overwrites python built-ins such as sum.
A complete example:
import numpy as np
from scipy.optimize import curve_fit
import uncertainties as unc
import matplotlib.pyplot as plt
import uncertainties.unumpy as unp
def func(x, a, b, c):
'''Exponential 3-param function.'''
return a * np.exp(b * x) + c
x, y = np.genfromtxt('data.txt', unpack=True)
popt, pcov = curve_fit(func, x, y)
a, b, c = unc.correlated_values(popt, pcov)
# Plot data and best fit curve.
plt.scatter(x, y, s=3, linewidth=0, alpha=0.3)
px = np.linspace(11, 23, 100)
# use unumpy.exp
py = a * unp.exp(b * px) + c
nom = unp.nominal_values(py)
std = unp.std_devs(py)
# plot the nominal value
plt.plot(px, nom, c='r')
# And the 2sigma uncertaintie lines
plt.plot(px, nom - 2 * std, c='c')
plt.plot(px, nom + 2 * std, c='c')
plt.savefig('fit.png', dpi=300)
Solution 3
Notice: the actual answer to obtaining the fitted curve's confidence interval is given by Ulrich here.
After some research (see here, here and 1.96) I came up with my own solution.
It accepts an arbitrary X% confidence interval and plots upper and lower curves.
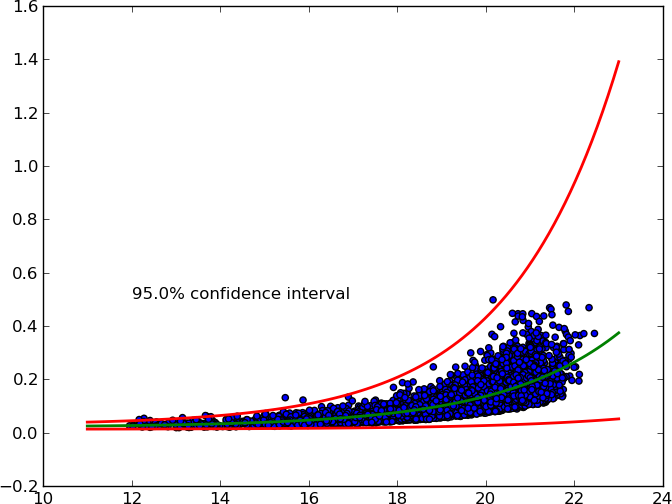
Here's the MWE:
from pylab import *
from scipy.optimize import curve_fit
from scipy import stats
def func(x, a, b, c):
'''Exponential 3-param function.'''
return a * np.exp(b * x) + c
# Read data.
x, y = np.loadtxt('exponential_data.dat', unpack=True)
# Define confidence interval.
ci = 0.95
# Convert to percentile point of the normal distribution.
# See: https://en.wikipedia.org/wiki/Standard_score
pp = (1. + ci) / 2.
# Convert to number of standard deviations.
nstd = stats.norm.ppf(pp)
print nstd
# Find best fit.
popt, pcov = curve_fit(func, x, y)
# Standard deviation errors on the parameters.
perr = np.sqrt(np.diag(pcov))
# Add nstd standard deviations to parameters to obtain the upper confidence
# interval.
popt_up = popt + nstd * perr
popt_dw = popt - nstd * perr
# Plot data and best fit curve.
scatter(x, y)
x = linspace(11, 23, 100)
plot(x, func(x, *popt), c='g', lw=2.)
plot(x, func(x, *popt_up), c='r', lw=2.)
plot(x, func(x, *popt_dw), c='r', lw=2.)
text(12, 0.5, '{}% confidence interval'.format(ci * 100.))
show()
Solution 4
curve_fit() returns the covariance matrix - pcov -- which holds the estimated uncertainties (1 sigma). This assumes errors are normally distributed, which is sometimes questionable.
You might also consider using the lmfit package (pure python, built on top of scipy), which provides a wrapper around scipy.optimize fitting routines (including leastsq(), which is what curve_fit() uses) and can, among other things, calculate confidence intervals explicitly.
Solution 5
I've always been a fan of simple bootstrapping to get confidence intervals. If you have n data points, then use the random package to select n points from your data WITH RESAMPLING (i.e. allow your program to get the same point multiple times if that's what it wants to do - very important). Once you've done that, plot the resampled points and get the best fit. Do this 10,000 times, getting a new fit line each time. Then your 95% confidence interval is the pair of lines that enclose 95% of the best fit lines you made.
It's a pretty easy method to program in Python, but it's a bit unclear how this would work out from a statistical point of view. Some more information on why you want to do this would probably lead to more appropriate answers for your task.
Admin
Updated on June 13, 2022Comments
-
 Admin about 2 months
Admin about 2 months