How to Calculate Double + Float Precision

Question

I have been trying to find how to calculate the Floating/Double precision/range numbers -3.402823e38 .. 3.402823e38 and -1.79769313486232e308 .. 1.79769313486232e308.

For int32 you would do 2^32=4294967296/2 you get a range of -2147483648 to 2147483647. So how do i figure out the precision numbers for float and double. I think i am searching the wrong terms since nothing is coming up anywhere.

Solution

Well, both types actually look like the following:

[sign] [exponent] [mantissa]

representing a number in the following form:

[sign] 1.[mantissa] × 2^[exponent]

with the size of the exponent and mantissa varying. For float the exponent is eight bits wide, while double has an eleven-bit exponent. Furthermore, the exponent is stored unsigned with a bias which is 127 for float and 1023 for double. This results in a range for the exponent of −126 through 127 for float and −1022 though 1023 for double.

The exponent is the exponent for 2^something so when calculating 2¹²⁷ you'll get 1.7 × 10³⁸ which gets you in the approximate range of the float maximum value. Similarly for double with 9 × 10³⁰⁷.

Obviously those numbers are not exactly those we expect. This is where the mantissa comes into play. The mantissa represents a normalized binary number that always begins with “1.” (that's the normalized part). The rest is simply the digits after the dot. Since the maximum mantissa is then roughly 1.111111111... in binary, which is almost 2, we'll get approximately 3.4 × 10³⁸ as float's maximum value and 1.79 × 10³⁰⁸ as the maximum value for double.

[EDIT 2011-01-06] As Mark points out below (and below the question), the exact formula is the following:

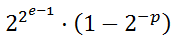
where e is the number of bits in the exponent and p is the number of bits in the mantissa, including the aforementioned implicit bit (due to normalization). The formula replicates what we have seen above, only now accurate. The first factor, 2^{2e − 1}, is the maximum exponent, multiplied by two (we save the two in the second factor then). The second factor is the largest number we can represent below one. I said above that the number is almost two. Since we exaggerated the exponent by a factor of two in this formula, we need to account for that and now have a number that is almost one. I hope it's not too confusing.

In any case, for float (with e = 8 and p = 24) we get the exact value 340282346638528859811704183484516925440 or roughly 3.4 × 10³⁸. double then yields (with e = 10 and p = 53) 179769313486231570814527423731704356798070567525844996598917476803157260780028538760589558632766878171540458953514382464234321326889464182768467546703537516986049910576551282076245490090389328944075868508455133942304583236903222948165808559332123348274797826204144723168738177180919299881250404026184124858368 or roughly 1.80 × 10³⁰⁸.

[/EDIT]

Another thing: You're bringing up the term “precision” in your question but you quote the ranges of the types. Precision is a quite different thing and refers to how many significant digits the type can retain. Again, the answer here lies in the mantissa which is 23 and 52 bits for float and double, respectively. Since the numbers are stored normalized we actually have an implicit bit added to that, which puts us at 24 and 53 bits. Now, the way how digits after the decimal (or binary here) point work is the following:

 1.   1     0     1     1
 ↑    ↑     ↑     ↑     ↑
2^0  2^-1  2^-2  2^-3  2^-4
 =    =     =     =     =
 1   0.5   0.25  0.125 0.0625

So the very last digit in the double mantissa represents a value of roughly 2.2 × 10⁻¹⁶ or 2⁻⁵², so if the exponent is 1, this is the smallest value we can add to the number – placing the double precision around 16 decimal digits. Likewise for float with roughly seven digits.

Comments

[Joey]

That's reiterating what the OP already knows and says, but doesn't explain how those numbers come to be.

[Joey]

−128 is not a valid exponent since those aren't stored as two's complement but instead unsigned with a bias added. Furthermore a zero exponent is reserved for subnormal numbers, further reducing the range. Also the exponent is for base 2, not 10. And the mantissa works differently as well.

[davogotland]

right.. forgot. thanks man! i'm just trying to get at the principle of how it's really the number of decimals that your program's purpose requires that will be the final factor for understanding the achievable range :) (i should have just written that right away, haha)

[Mark Dickinson]

You explain how to get to 'approximately 3.4 * 10^38'; why not go one step further and explain how to give the exact max value, namely 2^(2^(e-1)) * (1 - 2^p) for an IEEE 754 binary type with e bits for the exponent and p bits (including the hidden bit) for the mantissa?

[Joey]

@Mark: 3.402823e38 is still approx. 3.4e38 to me (and the exact value that [float]::MaxValue gives me. Thanks for the explicit formula, though, but it gives −5.7e45 instead of 3.4e38. 2^(2^(e − 1)) * (1 − 2^−p) would work. (Though now I'm at a loss to explain why there is “1 - 2^−p” and not “2 - 2−^p” like I explained in the post above (the part with "almost two"). Still too early today and if my reasoning in the post is plain wrong, please correct if you find a correctable mistake. I just went ahead explaining as good as I could due to other answers being wrong to downright silly.

[Joey]

@Mark: Nevermind, I understood now and edited it in. Thanks for the exact formula (I would have come up with one, but the laziness to go to Wolfram|Alpha to evaluate it won – don't have a CAS for quick-and-dirty bignum calculations here).

[Mark Dickinson]

Grr. Stupid fingers. :-) You're right, of course---I meant 2^-p, not 2^p. Thanks!

[Olof Forshell]

A very confusing answer. Second, the exponent (bias or not) is expressed in powers of two.

[Olof Forshell]

I pressed enter too quickly. This is a very confusing answer. First, with 24 bits you can express all integers from 0 to 16777215 (given a suitable index): if the value is negative or positive depends on the sign bit. Second, the exponent (bias or not) is expressed in powers of two. Third, the accuracy of the number does not "get lower" it's still 7-8 digits. BTW 7-8 digits of precision are most easily illustrated with 16777215: it obviously handles all 7-digit numbers (0-9999999) and in addition a (small) part of the 8-digit range. Ergo 7-8 digits.

[JASON]

One thing to point out. For "double" the exponent is 11-bits. en.wikipedia.org/wiki/Double_precision_floating-point_format

[Joey]

Thanks. I guess the bias of ~2^10 threw me off there. You could have suggested an edit too, by the way :)

[Royi Namir]

Joey , I cant find where do you see the bias which is 127 please look here i.stack.imgur.com/54mto.jpg - Bias according to where ? where is the bias ?

[Wandering Fool]

@Joey According to What every computer scientist should know about floating-point arithmetic, the leading 1 in binary floating point is part of the 24 bit mantissa for float and 53 bit mantissa for double as you said. However, you say at the end that the last digit in the double mantissa is 2^-53. This is incorrect because 2^-53 is the 54th bit which a double does not have. It should be 2^-52 or about 2.22E-16. I will submit an edit request with my explanation and have someone smarter than I verify it.

[Wandering Fool]

I really hope I'm wrong though, because having it be 2^-53 looks alot better.

[Joey]

@WanderingFool: It appears that you are right, indeed. The reviewers didn't think so, although none of them seem to have any expertise on the subject at hand. I'll add your edit.

[Mohit Shah]

Why do you say that exponent is stored unsigned and then say that range is -126 to 127. Its really confusing. Also if you could clear why it is not -127 go +127.